Visual Explorations of Sample Size
Drawing conclusion based on small samples is obviously problematic. At the same time, I also wonder whether the rise to prominence of "Big Data" can lead organisations to blindly collect as much data as possible rather than think logically about how much data is actually necessary to perform whatever analysis tasks are required.
Drawing conclusion based on small samples is obviously problematic. At the same time, I also wonder whether the rise to prominence of “Big Data” can lead organisations to blindly collect as much data as possible rather than think logically about how much data is actually necessary to perform whatever analysis tasks are required.
I’d rather have a bit more data than necessary than not quite enough, but that doesn’t mean we should be collecting everything just because we can. We can use statistics to guide us as to how much data we really need, but I recently got to thinking about how we can visually show what effect increasing the sample size has.
To keep things simple I’ll just look at the effect of increasing the sample size with random variates from a specific (but rather arbitrary) instance of the normal distribution. I will leave stating the parameters – the true mean and true standard deviation – till later.
The animated gif below shows probability density histograms made from sampling the aforementioned normal distribution. From frame to frame the sample size increase by a factor of ten and the data used to draw each histogram is a superset of the data in the previous frame. The red curve is the normal distribution with the same mean and standard deviation as the sample data.
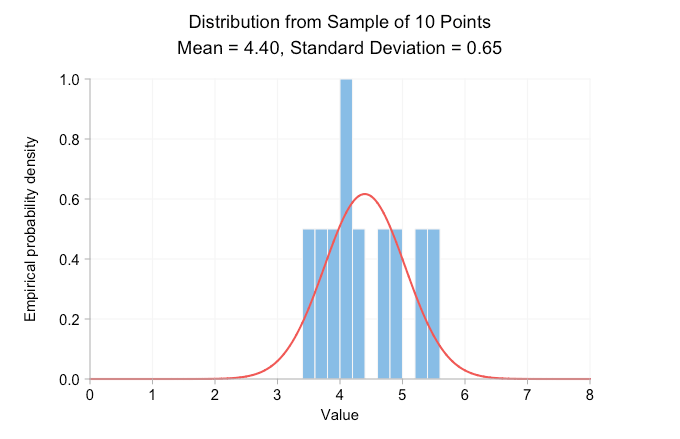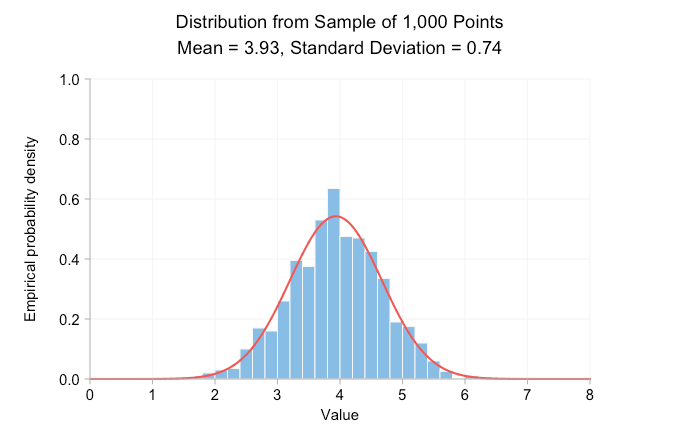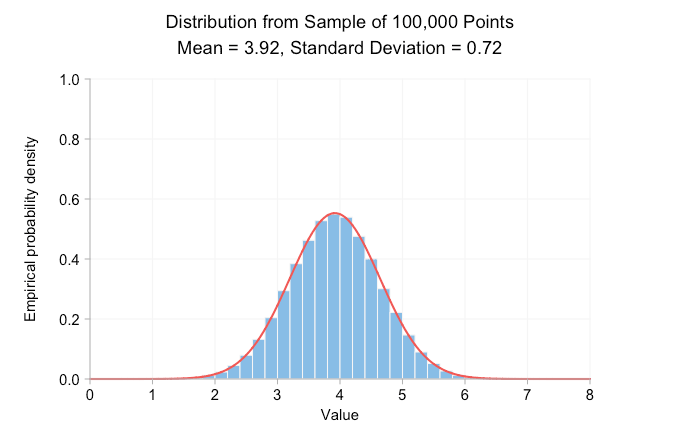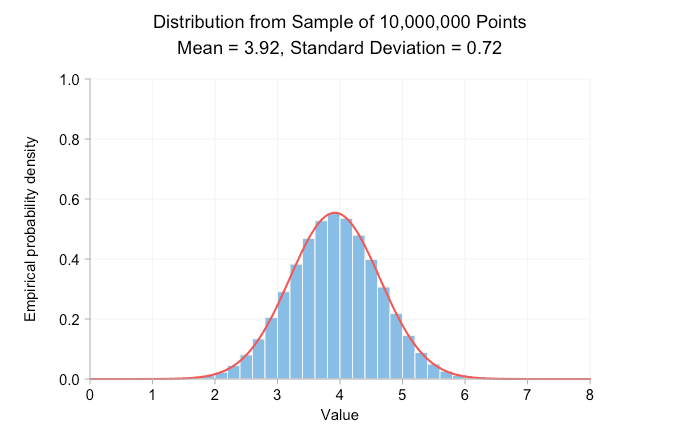
Clearly, with a sample size of just ten, the empirical distribution looks nothing like the normal distribution with the same mean and standard deviation. All we can really say from this is that the true mean is likely somewhere close to 4 or 5. But increase the sample to 100 points and we can already see a rough bell-curve. By the time we’ve made it to 100,000 points we have a very good visual match between histogram and curve. Adding more points doesn’t change the look of the distribution or the printed mean and standard deviation.
The animated histogram is good at giving a broad overview of how things change as we add more points, but with only one frame for every factor of 10 we don’t see a very detailed picture. Without printing more digits in the parameters of the title at the top, it’s not clear just how precisely we know the mean and standard deviation for any particular sample size. For a better idea of this we can pick a parameter and plot that as a function of the sample size, from 2 points (when both sample parameters are finite) up to ten million. We’ll look at the mean first.
Because things change much more quickly when there’s only a small amount of data, the above chart is pretty useless. Taking the (base 10) logarithm of the number of points in the sample makes things much clearer.
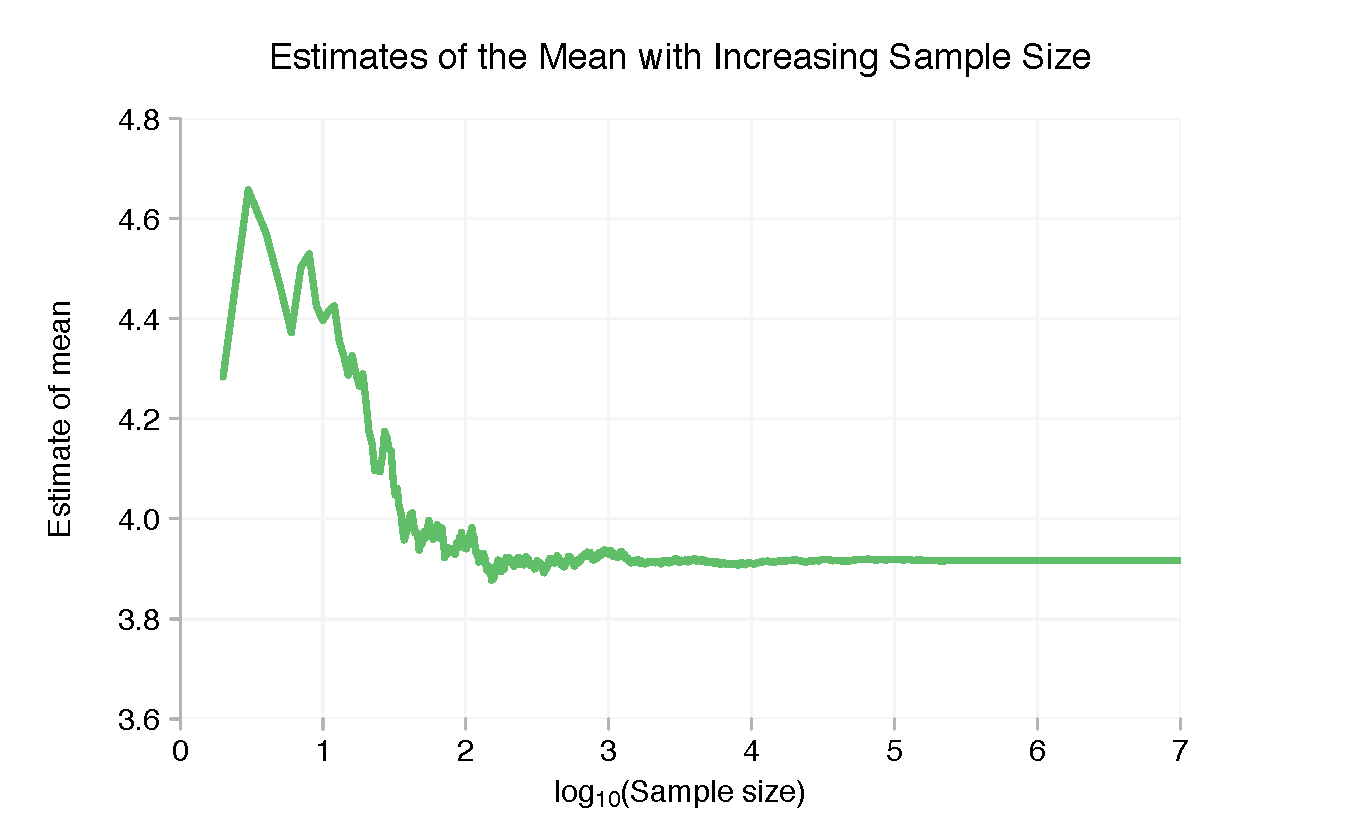
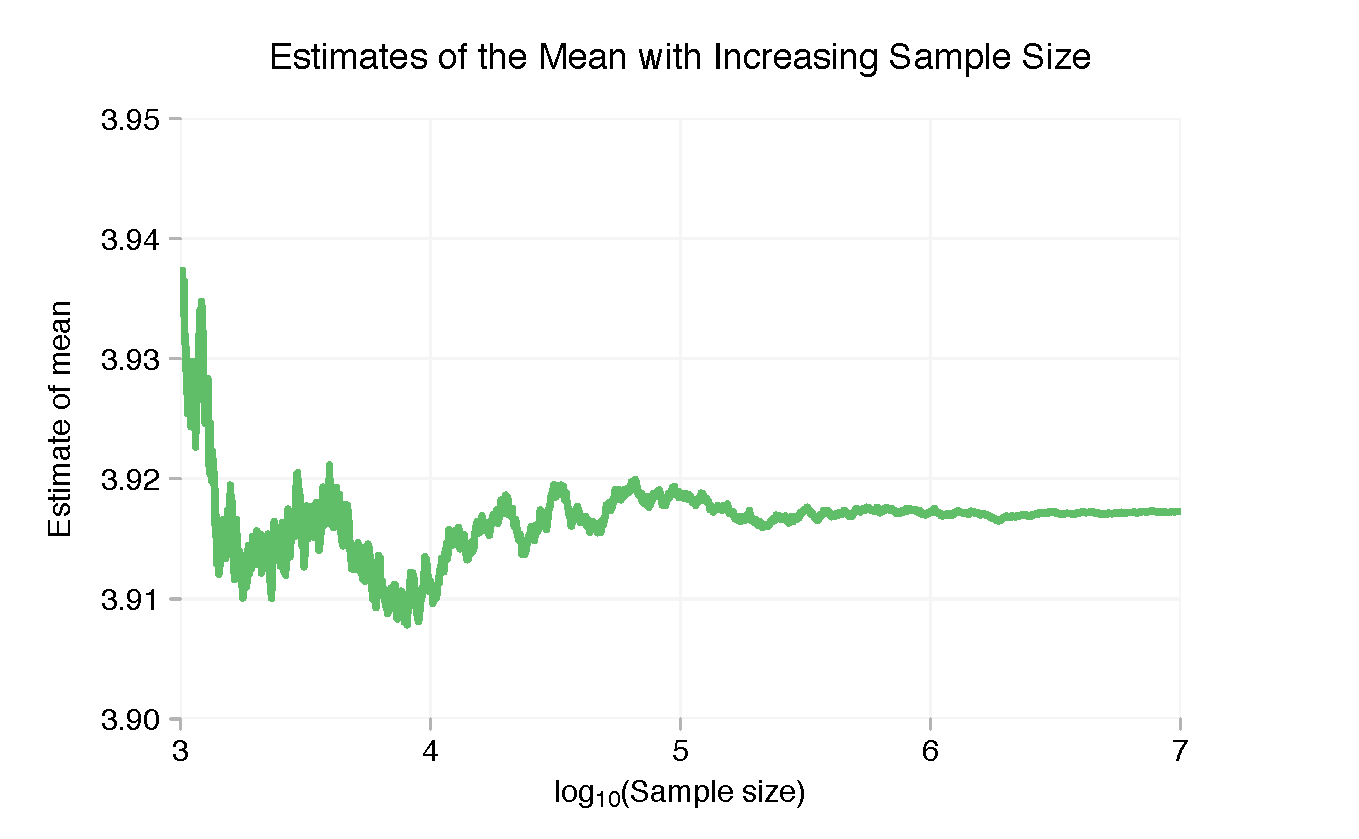
With only a few points the sample mean is well above 4. But this quickly drops and stabilises once we’re in to double digits. Beyond a few thousand points there’s little discernible variation in the sample mean, but we can zoom in on the right-hand side and see the finer “wobble”.
Here’s how the standard deviation changes as we change the sample size (note: this is the standard deviation of the sample, not the standard error of the mean!):
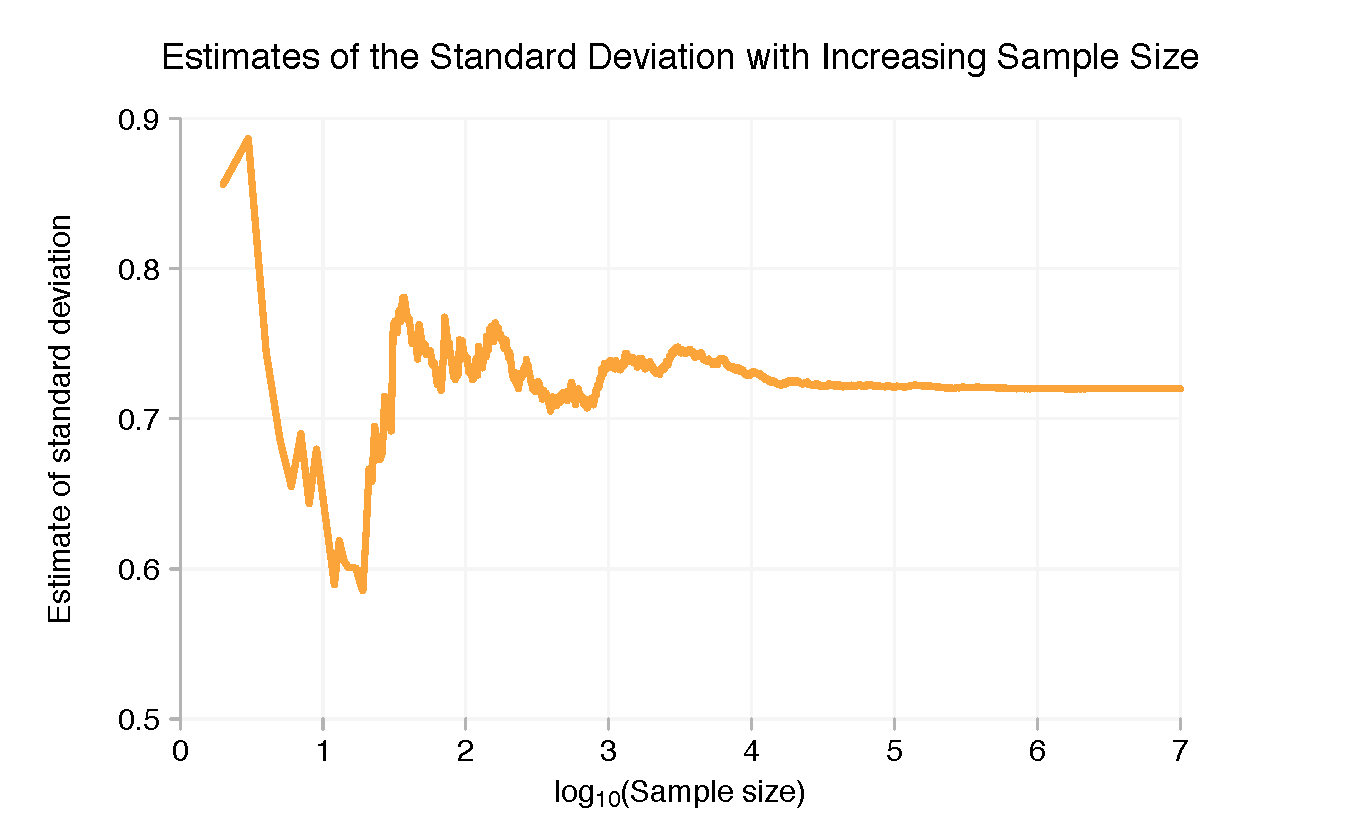
The true mean used to generate the sample was 3.9172 and the standard deviation was 0.7200. We can see from the charts that we’ve got pretty close to these numbers with ten million data points without doing any rigorous statistical analysis. But we weren’t that far away at ten thousand data points either. More data means more precision, but if all you needed to know was whether the mean was more or less than 4, ~1,000 points would have been enough.
To reinforce the point, let’s look at just the first 100,000 data points and break these up into ten samples of 10,000. With each subsample we can use the same graphical technique as before. The coloured lines in the charts below show the results for the first 10,000 data points, the grey lines the other subsamples.
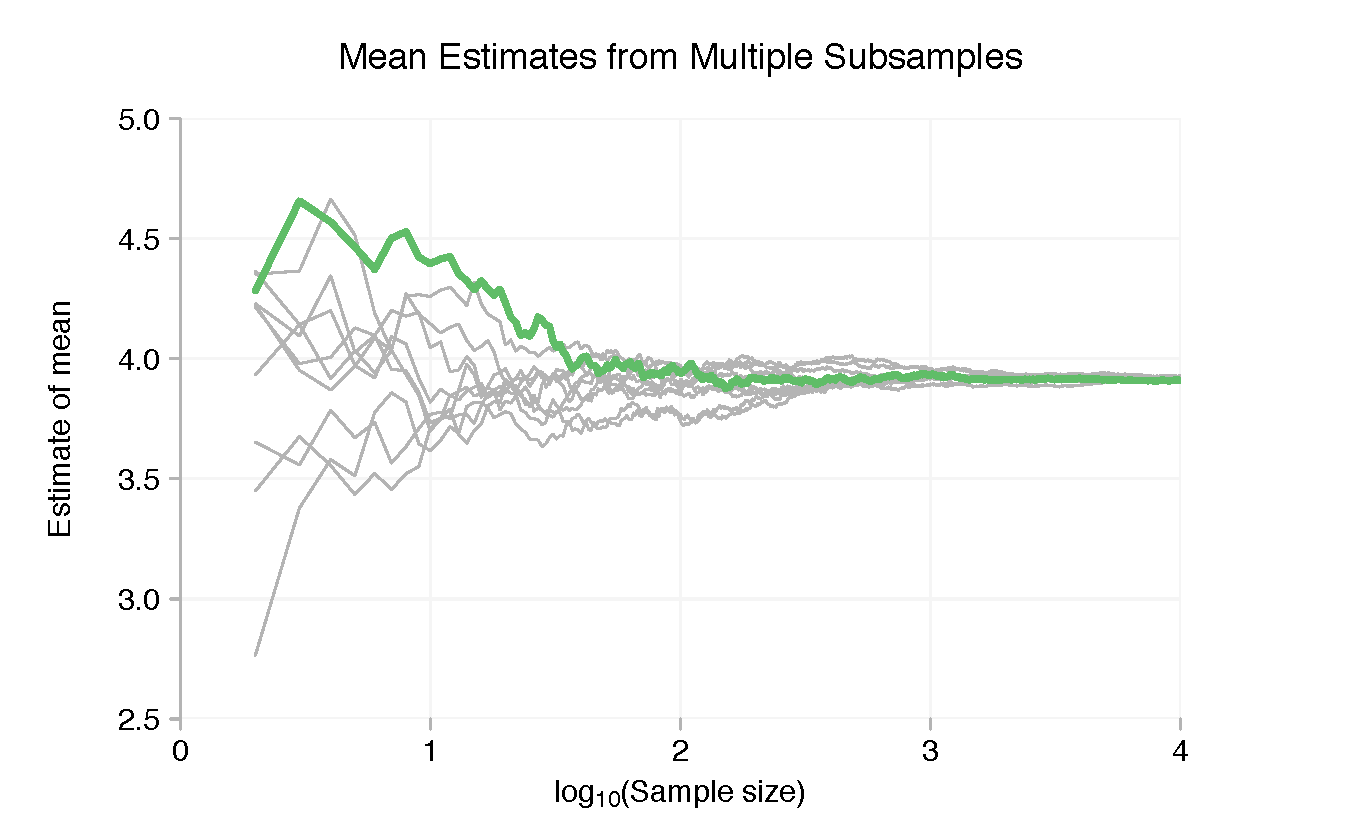
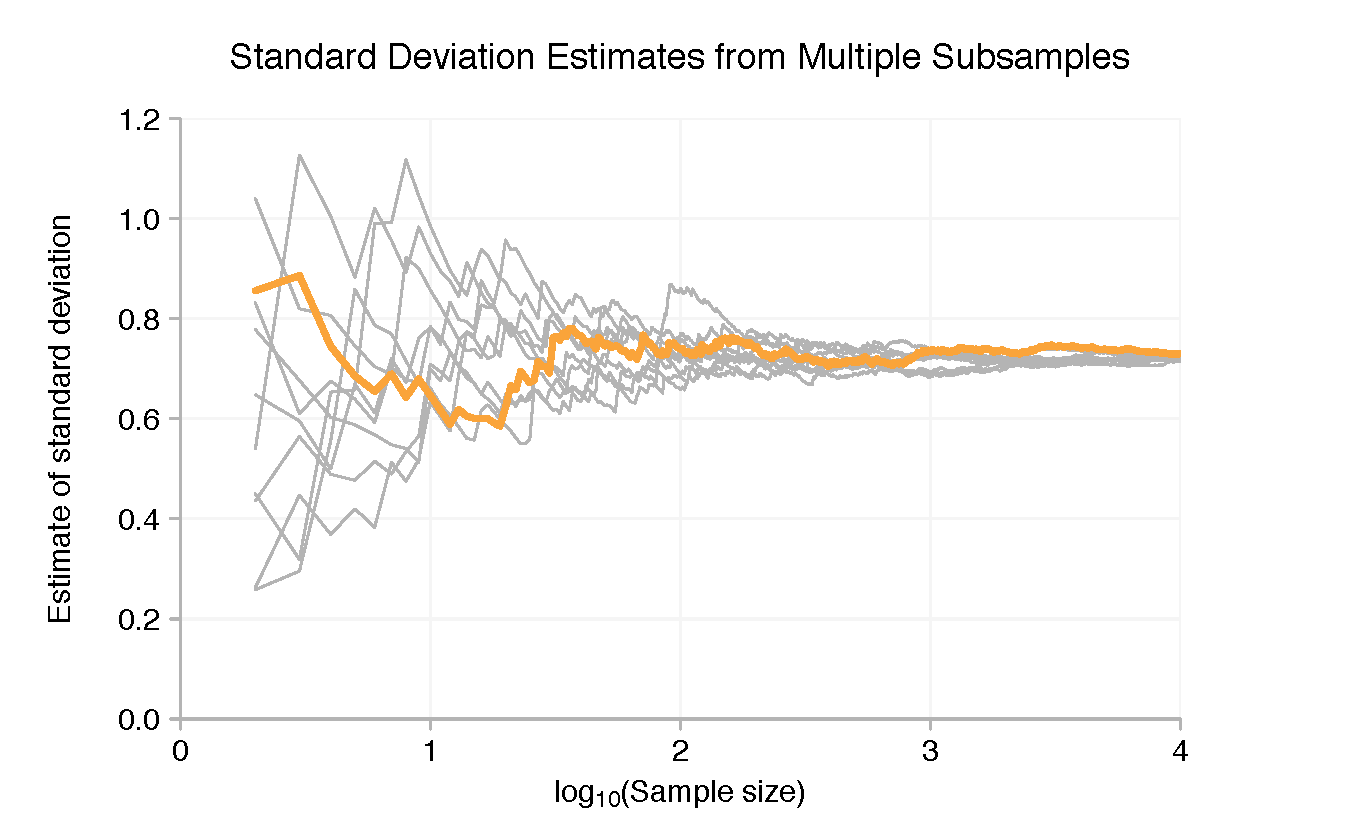
To be clear, the purpose of the charts isn’t really to see the individual tracks made by one subsample. It’s to show that the means and standard deviations of the subsamples are spread widely when each has only a few data points but, at least on a logarithmic scale, quickly converge as we add more points.
Of course all datasets are different and many don’t come about through simple random sampling. Neither can you assume your real-world dataset will be as well-behaved as a large collection of computer-generated random variates from a single instance of the normal distribution. Moreover, the chart ideas above aren’t meant as straight replacements for rigorous statistics work. But in certain cases they may complement it, e.g. by providing a sanity check of a statistical assessment or as a visual alternative for an audience with less technical expertise.
Looking for a comprehensive and rapid prototyping tool, which allows you to see exactly how your build will look and work before even writing a single code of line? Look no further. Download our Indigo Studio free trial now and see what it can do for you!
